Random variable of interest ap stats – Random variables play a pivotal role in AP Statistics, providing a framework for understanding and analyzing the behavior of data. This comprehensive guide delves into the definition, types, and applications of random variables, equipping readers with a solid foundation for statistical inference.
From discrete to continuous distributions, we explore the characteristics and properties of different types of random variables. We delve into sampling methods and probability distributions, laying the groundwork for understanding the behavior of data.
Definition of Random Variable of Interest
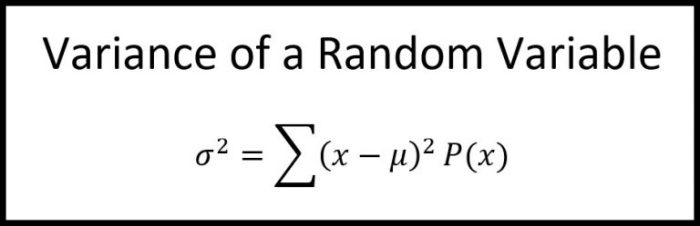
A random variable is a numerical characteristic of a population or sample that can take on different values. It is a function that assigns a numerical value to each element in the sample space. Random variables are used to represent the outcomes of random experiments or processes, and they play a crucial role in statistics.
There are different types of random variables, including discrete, continuous, and mixed. Discrete random variables can take on only a finite or countable number of values, while continuous random variables can take on any value within a specified range. Mixed random variables are a combination of both discrete and continuous variables.
Random variables are essential for statistical analysis because they allow us to quantify and analyze the variability in data. They are used in a wide range of applications, such as hypothesis testing, confidence intervals, and regression analysis.
Types of Random Variables: Random Variable Of Interest Ap Stats
Discrete Random Variables
Discrete random variables can take on only a finite or countable number of values. Examples of discrete random variables include the number of heads obtained when flipping a coin, the number of customers visiting a store on a given day, and the number of defects in a manufactured product.
Continuous Random Variables
Continuous random variables can take on any value within a specified range. Examples of continuous random variables include the height of individuals in a population, the weight of a newborn baby, and the time it takes for a customer to be served at a restaurant.
Mixed Random Variables, Random variable of interest ap stats
Mixed random variables are a combination of both discrete and continuous variables. An example of a mixed random variable is the outcome of a roll of a die, which can be either a discrete value (1, 2, 3, 4, 5, or 6) or a continuous value (any number between 1 and 6).
Sampling and Probability Distributions

Sampling is the process of selecting a subset of a population to represent the entire population. Probability distributions are mathematical functions that describe the probability of different outcomes occurring in a random experiment or process.
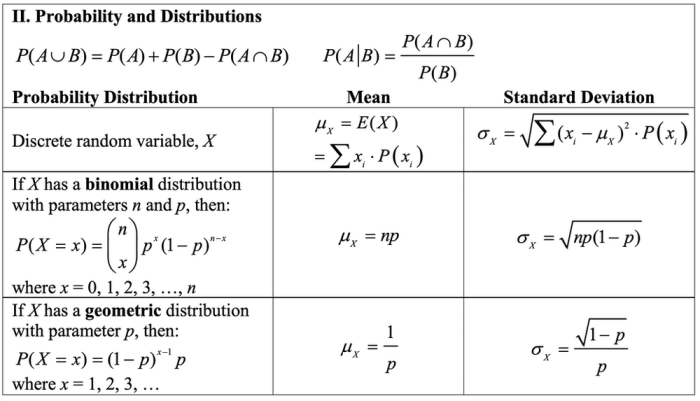
The probability distribution of a random variable is determined by its type. Discrete random variables have a probability mass function, which gives the probability of each possible value. Continuous random variables have a probability density function, which gives the probability of a value falling within a given interval.
Expected Value and Variance

Expected value, also known as mean, is a measure of the central tendency of a random variable. It is the average value that the random variable is expected to take on over a large number of trials.
Variance is a measure of the spread or dispersion of a random variable. It is the average of the squared deviations from the expected value.
Expected value and variance are important concepts in statistics because they provide information about the distribution of a random variable. They are used in a wide range of applications, such as hypothesis testing, confidence intervals, and regression analysis.
Hypothesis Testing
Hypothesis testing is a statistical procedure used to determine whether there is evidence to support a particular claim about a population.
The steps involved in hypothesis testing include:
- Stating the null hypothesis and alternative hypothesis
- Collecting a sample from the population
- Calculating the test statistic
- Determining the p-value
- Making a decision
Random variables play a crucial role in hypothesis testing. The test statistic is a random variable that is used to determine the p-value. The p-value is the probability of obtaining a test statistic as extreme as or more extreme than the one that was observed, assuming that the null hypothesis is true.
Applications in Statistical Inference
Random variables are used in a wide range of applications in statistical inference, including:
- Confidence intervals
- Hypothesis testing
- Regression analysis
- Bayesian analysis
Random variables allow us to make inferences about a population based on a sample. For example, we can use confidence intervals to estimate the true mean of a population with a certain level of confidence. We can also use hypothesis testing to determine whether there is evidence to support a particular claim about a population.
Question & Answer Hub
What is a random variable?
A random variable is a function that assigns a numerical value to each outcome of a random experiment.
What are the different types of random variables?
There are two main types of random variables: discrete and continuous. Discrete random variables take on a finite or countable number of values, while continuous random variables can take on any value within a specified range.
What is the expected value of a random variable?
The expected value of a random variable is the average value that the random variable would take on over many repetitions of the experiment.
